圖5. 器件非線性度。

其中：

AMEA為給定gn下的測得加速度。

AFIT 為給定gn下的預測加速度。

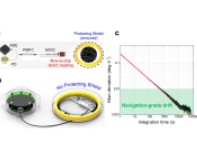
多數加速度計或組合器件在給定輸入加速度計范圍內均存在非線性——例如，30 mg± 2g的范圍。對于傾角測量應用，輸入坡道斜率在±30°以內，這意味著輸出加速度范圍在±500 mg (±1g× sin 30°)以內，所以應重新評估該范圍內的非線性度。由于非線性度在整個輸入范圍內是非線性的，所以，很難準確地量化評估這部分誤差。然而，由于該器件的數據手冊通常都很保守，線性度為30 mg，輸入范圍為±2g，用10 mg計算±500 mg范圍內的誤差更合理些。

與初始絕對失調的總失調變化

與初始絕對失調的總失調變化為溫度、應力和老化效應導致的失調的最大偏差。該偏差是相對于給定器件的初始絕對失調進行測量的。這是精度總誤差的主要貢獻因素。

在溫度、應力、老化等所有這些因素中，變化與溫度在總失調變化中占比很大。一般地，變化與溫度曲線是二階曲線，通常為旋轉拋物線。為了消除這部分誤差，可以在系統級執行三點校準。對于給定器件，可按下列步驟校準輸出失調隨溫度的變化值。

第1步：

使器件的輸出響應以某個 ?N0值偏移。溫度校準流程的第一步是 消除環境溫度下的失調。

圖7. 第2步：在消除環境溫度下的失調之后。

第2步：

接下來，在高溫下測試器件，用獲得的新信息生成失調校正線性公式。

圖9. 第4步：在消除高溫下的拋物線旋轉分量之后。

第3步：

給現有公式添加一個二階分量，校正失調剩余部分。設二階曲線遵循以下公式：

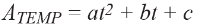
這是二階拋物線公式，已經通過第1步和第2步消除了旋轉分量。

在該公式中，該二階拋物線有三個解：

然后，我們可以得到溫度系數 a, b, c.