FFT(Fast Fourier Transformation)簡稱為快速傅里葉變換，是DFT(Discrete Fourier Transform)離散傅里葉變換的一種快速算法。DFT是一種常用的信號處理方式，可以將時域信號轉到頻域。但是因為DFT運算復雜度太高，在實際應用中都是采用FFT的快速算法。

簡單來說，示波器的FFT功能就是利用傅里葉變換經過系統的運算，將波形從時域變換成頻域的方法。原來的輸入信號經過傅里葉變換后得到的波形稱為頻譜。

傅里葉分析不僅僅是一個數學工具，更是一種可以徹底顛覆一個人世界觀的思維方式。但是傅里葉分析公式看起來太復雜，令許多人望而卻步，這次我們嘗試用另外一種有趣的方式來解釋傅里葉分析。

什么是時域

我們從呱呱落地出生，睜開眼睛的一刻開始，所看到的世界都是以時間貫穿的，天空上云朵漂浮的軌跡，宇宙中地球的公轉與自轉，軌道上火車的行駛路程都會隨著時間發生改變。這種以時間為橫坐標軸作為參照來觀察動態世界的方法我們稱之為時域分析。示波器上的電信號也是如此，電壓的大小隨時間變化，這就是時域，我們可以從下面一個圖(1-1)直觀的看出來。

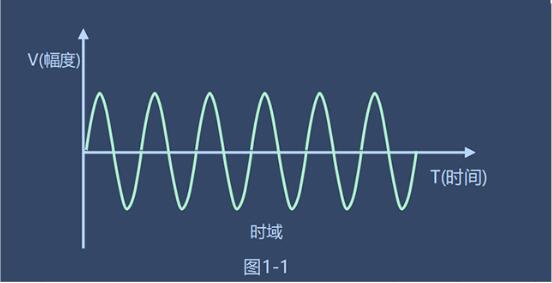
什么是頻域

相對于時域，頻域是以頻率作為橫坐標的參考系去觀察世界。我們可以想象一下，我們的手機正在播放一首流行音樂，隨著時間的的推移，音樂正在按部就班地按照音譜播放著，此時若以歌曲的高低音作為縱軸，時間作為橫軸建立直角坐標系得到(圖1-2)；以音譜作為橫坐標軸建立直角坐標系得到(圖1-3)，我們可以將圖（1-2）理解為時域，圖（1-3）理解為頻域，信號由時域轉換成頻域的過程，我們稱之為傅里葉變換。

理解傅立葉變換基本原理

傅里葉變化認為，任何一個原始的周期函數，都可以用多個正余弦波疊加而成，隨著疊加的遞增，所有正弦波中上升的部分逐漸讓原本緩慢增加的曲線不斷變陡，而所有正弦波中下降的部分又抵消了上升到最高處時繼續上升的部分使其變為水平線，一個矩形就這樣疊加而成了。

將以上所述繪制成一幅圖片，我們就可以輕而易舉的從時域和頻域的角度去觀察我們所測試的波形。

示波器FFT頻譜分析的作用

既然示波器FFT頻譜分析功能強大易用，那經典的應用場景有哪些呢？例如說，當電子研發工程師在測試實際電路時，電路上的信號被噪聲干擾了，此時會對電路產生干擾震蕩，此時想去掉這個噪聲。在時域波形上看，只能看出是一個密集的上躥下跳的噪聲，毫無規則可言，完全看不出有其他有用的信息有助于改善噪聲。此時使用FFT頻譜分析，可以明顯的看出噪聲分布的頻率范圍，就可以得知在電路中是哪個芯片或者元器件造成噪聲，此時就可以有針對性的對造成噪聲的電路進行濾波處理。

在音頻應用中，通過人體的耳朵很難標準化的分辨出一些音頻的頻率范圍。使用FFT頻譜分析對音頻處理單元信號進行分析，可以準確測量音頻響應的頻譜范圍，從而快速確定音頻單元是否符合規范。

窗函數及類型

? 柵欄效應

柵欄效應是指對一函數進行采樣，即是抽取采樣點上的對應的函數值。其效果如同透過柵欄的縫隙觀看外景一樣，只有落在縫隙前的少數景象被看到，其余景象均被柵欄擋住而看不到，這種現象稱為柵欄效應。

由于柵欄效應對頻域采樣影響很大，會使采集的頻域信號丟失頻率成分或是具有重要特征的成分，因此在測試時必須先擇正確的窗函數。