一階模型的質(zhì)量取決于時域波形的精確形狀和帶寬定義，對于 100 MHz 頻率的合成方波，僅將前 9 個諧波加在一起的合成信號的帶寬為 0.9 GHz，測得的 10% 到 90% 上升時間為 0.39 ns。具有特定形狀的誤差函數(shù)邊沿信號（高斯積分）的10% 至 90% 上升時間也是 0.39 ns（參考下圖），信號的形狀不完全相同但相似，應(yīng)該具有相似的帶寬。

上升時間為 0.39 ns的誤差函數(shù)信號的頻譜看起來也像通過 一階濾波器的理想方波的頻譜（參考下圖）。信號帶寬 0.9 GHz 處的頻率分量幅度也比理想方波低 3 dB，并且，在 0.9 GHz 以上，誤差函數(shù)邊沿信號的頻率分量下降速度超過 20 dB/十倍頻程。和在合成波形中一樣，在極點頻率之上，幅度是微不足道的。

說明濾波器的極點頻率是確定時域中重建波形所需的最高頻率分量的有用近似值。然而，這只是一個近似值。

這就是經(jīng)驗公式的來源，例如，1 ns上升時間信號的帶寬為 0.35/1 ns = 350 MHz。鑒于帶寬的這種近似值，壓擺率是多少？

上升時間和壓擺率

信號的壓擺率是電壓波形的斜率，即電壓的變化率。對于一階，壓擺率為：

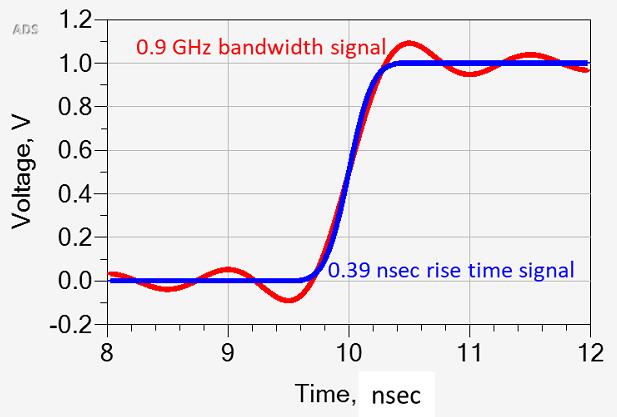
可以通過改變電壓變化幅度來創(chuàng)建具有與上升時間無關(guān)的壓擺率的信號，例如，在文章開始的圖中顯示了兩個波形。它們具有相同的 10% 到 90% 的上升時間，均為 10 ns，但較大的幅度是較小幅度的 5 倍。因此，較大波形的壓擺率是較小波形的 5 倍。

較大幅度的信號具有更大的 dV/dt，看起來它的頻譜中應(yīng)該有更高的頻率分量以產(chǎn)生更大的斜率，但上升時間是相等的。當波形的幅度縮小時，頻譜分量的幅度也縮小。對于相應(yīng)的理想方波，幅度下降 3 dB 的頻率是相同的（見下圖）。因此，兩個波形的帶寬是相同的。

每個波形的帶寬與頻譜的形狀有關(guān)，而不是頻率分量的絕對幅度。重建具有較大幅度的有限上升時間方波與小幅度信號需要相同的頻率分量，每個分量只是具有較大的幅度。重建每個波形所需的最高頻率分量是相同的。

總結(jié)

時域中的每個信號在頻域中都有自己對應(yīng)的頻譜。對于理想方波，很容易計算其頻譜分量及其幅度。要創(chuàng)建具有 0 ps 上升時間的理想方波，需要無窮的正弦頻率分量。盡管這些分量的幅度隨著頻率的提高而變得越來越小，但要創(chuàng)建一個較短的上升時間。每個分量都需要的，頻率分量的絕對幅度不是決定其帶寬的因素。

在合成有限上升時間的方波時，不需要帶寬以上的頻率分量來重新創(chuàng)建上升時間。根據(jù)經(jīng)驗，發(fā)現(xiàn)該帶寬接近于常用的基于一階濾波器階躍響應(yīng)的信號帶寬模型。

信號的頻譜取決于波形的精確形狀。實際上，該頻譜可由一階濾波器的階躍響應(yīng)近似。極點頻率是幅度比理想方波下降 3 dB 的頻率，此后更高頻率分量的貢獻可以忽略不計。

由于影響帶寬的是信號的上升時間，因此電壓變化的斜率不是影響的因素。如果信號的幅度信號加倍，則壓擺率加倍，每個諧波分量的幅度也加倍。但頻率分量下降 3 dB， 并且之后下降得更快的頻率點是相同的。