PTS-系列之PEK-100系列教學(xué)

PEK-130模塊之

三相正弦脈寬調(diào)變逆變器

寫在前面的話

經(jīng)過前幾期對(duì)于PTS-800中基本的電路圖拓?fù)浣Y(jié)構(gòu)的學(xué)習(xí)，我們已經(jīng)掌握了基本的電路模型。從PEK-100系列開始，在固有電路拓?fù)浠A(chǔ)上開始對(duì)電路的控制方式進(jìn)行學(xué)習(xí)。本期將針對(duì)直流變換器PEK-130對(duì)三相逆變器的數(shù)字控制進(jìn)行教學(xué)與分析，為老師提供符合教學(xué)目標(biāo)的實(shí)驗(yàn)設(shè)備。

PEK-130

三相逆變器模組

簡 述：

SPWM正弦脈寬度調(diào)變技術(shù)原理為由控制器產(chǎn)生的三相正弦波電壓命令與三角波做比較，經(jīng)過比較器，產(chǎn)生脈寬調(diào)變訊號(hào)驅(qū)動(dòng)逆變器，并使其輸出近似正弦波且為等幅不等寬的電壓波形。根據(jù)正弦波電壓和三角波的大小和頻率，可定義為下列兩個(gè)指標(biāo)，其一為調(diào)變指標(biāo) (Modulaton Index)為：

式中Vcontrol為三相正弦波電壓峰值大小，Vtri為三角波峰值的大小。

其二為頻率調(diào)變比(Frequency modulation ratio)，定義為：

式中fs為三角波頻率，f1為正弦波電壓頻率。

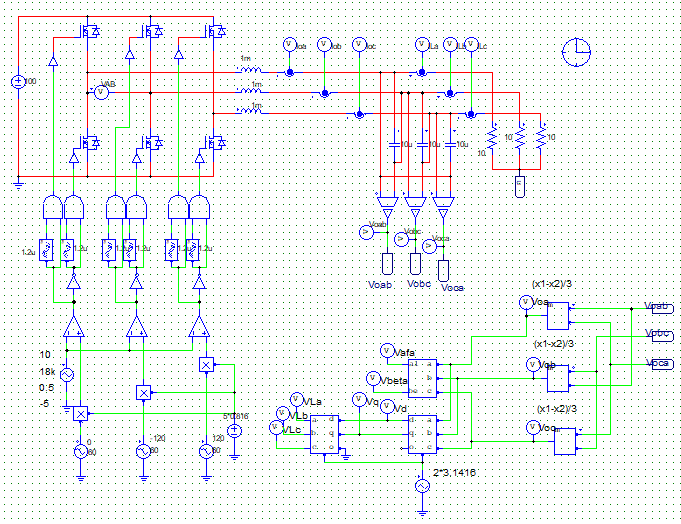
上圖為三相逆變器電路圖

三相SPWM：

以A相為例，電壓VAN其基本波的峰值可用下式表示：

基本波線-線電壓大小(RMS)為：

當(dāng)ma≤1時(shí)，稱為逆變器的線性調(diào)變區(qū)，亦即當(dāng)輸入正弦波電壓命令的峰值比三角波峰值小時(shí)，輸入電壓大小會(huì)與逆變器輸出電壓基本波的線-線電壓大小成正比。其三角波與正弦波如下圖所示：

三相空間向量SVPWM：

空間向量脈寬調(diào)變即是利用電壓空間向量的觀念，即由逆變器之六個(gè)功率組件的開關(guān)切換狀態(tài)來產(chǎn)生旋轉(zhuǎn)的電壓向量空間，典型的三相變頻器如圖所示，其每相各有兩個(gè)開關(guān)組件置于上臂及下臂，分別為上臂的S1、S3、S5及下臂的S2、S4、S6。在空間向量脈寬調(diào)變的控制模式下，逆變器每相開關(guān)組件的導(dǎo)通狀態(tài)為互補(bǔ)式，即代表若上臂導(dǎo)通則下臂截止，反之若上臂截止則下臂導(dǎo)通。在控制上通常在開關(guān)導(dǎo)通前加入一延遲時(shí)間以避免上臂與下臂功率組 件同時(shí)導(dǎo)通造成功率組件的損壞，此一延遲時(shí)間稱之為死區(qū)時(shí)間。在此定義開關(guān)導(dǎo)通狀態(tài)a、b、c相每一臂之開關(guān)導(dǎo)通狀態(tài)，若a=1則代表上臂開關(guān)導(dǎo)通下臂開關(guān)截止，a = 0則代表上臂開關(guān)截止下臂開關(guān)導(dǎo)通。因此三相逆變器之輸出狀態(tài)共有八種，每一種狀態(tài)產(chǎn)生的線對(duì)線電壓，相電壓之輸出結(jié)果(直流鏈電壓為VDC)列于下表。

由上表可以得知，三相逆變器輸出之相電壓和線間電壓之關(guān)系，經(jīng)由坐標(biāo)軸轉(zhuǎn)換至αβ平面上可得下表，其轉(zhuǎn)換之關(guān)系式為：

因此即由此八種開關(guān)切換狀態(tài)將可得到八種不同的電壓向量。此八個(gè)電壓向量稱為基本電壓向量，分別為六個(gè)有效電壓向量V1、V2、V3、V4、V5、V6及兩個(gè)零向量V0及V7。因此可利用此六個(gè)有效電壓向量將電壓空間平面分為六個(gè)區(qū)間，如下圖所示。其中αβ平面之α軸及β軸乃相對(duì)于交流馬達(dá)定子之水平軸及垂直軸， Vref則為輸出之參考電壓向量。

任何大小之輸出之參考電壓Vref可以用圖中六個(gè)有效電壓向量中之任兩個(gè)向量表示，而此輸出電壓在這兩個(gè)有效電壓向量之分量(導(dǎo)通時(shí)間)可用代數(shù)方法求得。

軸轉(zhuǎn)換：

靜止坐標(biāo)軸轉(zhuǎn)換：

將三相abc靜止坐標(biāo)軸轉(zhuǎn)換至αβ靜止坐標(biāo)軸系統(tǒng)，此轉(zhuǎn)換稱為Clark轉(zhuǎn)換。依據(jù)下圖所示兩個(gè)坐標(biāo)系統(tǒng)之間的關(guān)系，得出如下式的坐標(biāo)轉(zhuǎn)換式：

fa、fb、fo為電壓及電流等在αβ軸下的變數(shù)量

fa、fb、fc為電壓及電流等在abc軸下的變數(shù)量

反之，將坐標(biāo)軸αβ轉(zhuǎn)換至三相abc坐標(biāo)系統(tǒng)，此轉(zhuǎn)換稱為反Clark轉(zhuǎn)換，轉(zhuǎn)換公式可表示：

以上為由三相abc坐標(biāo)系統(tǒng)與靜止坐標(biāo)系統(tǒng)之間關(guān)系式，其轉(zhuǎn)換矩陣前的未定系數(shù)，若是采用非功率不變法則此為3/2，

若是采用功率不變法則此為

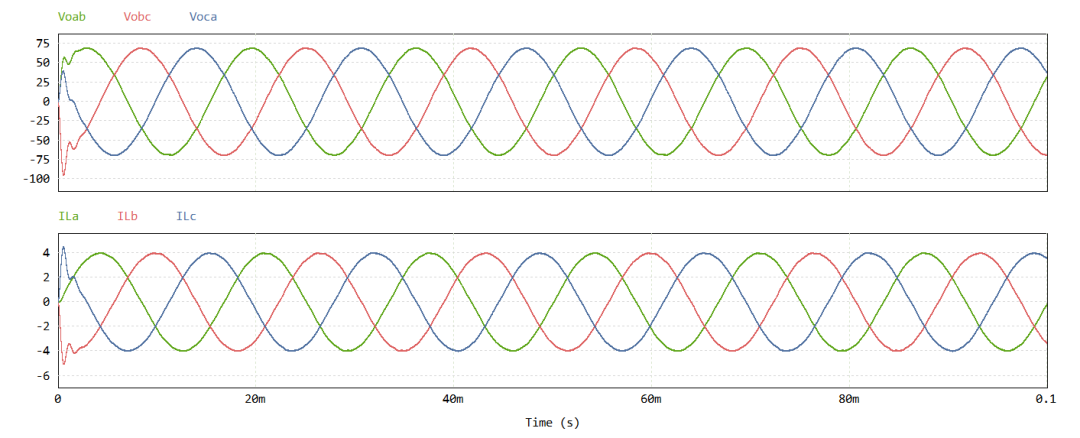
本文是采用非功率不變法則。此外，對(duì)于三相平衡系統(tǒng)，因此在做靜止坐標(biāo)軸轉(zhuǎn)換時(shí)，零序分量是可被忽略的。下圖是采用PSIM仿真abc靜止坐標(biāo)軸轉(zhuǎn)換至αβ靜止坐標(biāo)軸之波形圖。

同步旋轉(zhuǎn)坐標(biāo)軸轉(zhuǎn)換：

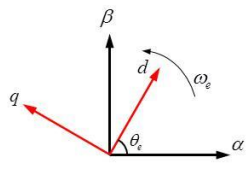
前一節(jié)透過坐標(biāo)軸轉(zhuǎn)換將abc靜止坐標(biāo)系統(tǒng)轉(zhuǎn)換至ab靜止坐標(biāo)軸系統(tǒng)，本節(jié)進(jìn)一步將αβ靜止坐標(biāo)軸轉(zhuǎn)換至DQ同步旋轉(zhuǎn)坐標(biāo)軸系統(tǒng)，此轉(zhuǎn)換稱為Park轉(zhuǎn)換，此時(shí)假設(shè)三相系統(tǒng)為平衡，零軸分量可被忽略，并將DQ軸與αβ軸同時(shí)放在二維向量平面上，如圖3.7 所示，此旋轉(zhuǎn)坐標(biāo)以ωe角速度來旋轉(zhuǎn)，故可得坐標(biāo)轉(zhuǎn)換公式：

其中：

反之，將旋轉(zhuǎn)坐標(biāo)系統(tǒng)DQ軸轉(zhuǎn)換至ab坐標(biāo)系統(tǒng)，此轉(zhuǎn)換稱為反Park轉(zhuǎn)換，則轉(zhuǎn)換公式可表示：

實(shí)驗(yàn)驗(yàn)證：

總　結(jié)：

基于三相逆變器變換器的數(shù)字控制是電力電子專業(yè)的必備課程，適用于本科及研究生階段對(duì)逆變器的學(xué)習(xí)與應(yīng)用。固緯電子在點(diǎn)力電子教學(xué)方向致力于為老師減少壓力，緩解學(xué)生的學(xué)習(xí)壓力，因此開創(chuàng)了全新的理論與實(shí)踐相結(jié)合的教學(xué)模式，還請各位老師同學(xué)進(jìn)行了解轉(zhuǎn)發(fā)。