Lamb(蘭姆)波是二維波,與三維體波相比具有衰減速度慢,傳播距離遠的特點,因此常被用于大型板材的長距離及快速無損檢測中。板材中蘭姆波與管中、變截面波導介質中的導波一樣,具有頻散性與多模態性。加上環境噪聲等多方面因素的影響,導波檢測時傳感器接收到的Lamb波信號非常復雜,屬于非平穩隨機信號,需要利用有效的信號處理技術提取有用的信息成分才能確定合適的激勵方式,獲得更好的檢測成像效果。傳統的處理Lamb波信號的方法包括反射系數法、傅里葉變換法、小波變換法、動態光彈法等,但是這些方法都有各自的不足。反射系數法是通過測量漏蘭姆波的頻散曲線來確定材料的性質,但測量難度較大。傅里葉變換只能處理線性非平穩的信號。小波變換法雖然在理論上能處理非線性非平穩信號,但是同傅里葉變換、短時傅里葉變換法一樣,都受Heisenberg測不準原理制約,即時間窗口與頻率窗口的乘積為一個常數,這就意味著如果要提高時間精度就得犧牲頻率精度,反之亦然。當蘭姆波中不同模態的頻率比較接近時,不適用小波變換處理信號。動態光彈法能從Lamb波的應力分布觀察到傳播和頻散,但是在實際檢測中對硬件要求較高。
HilbertGHuang變換(HHT)是一種近幾年發展起來的一種自適應信號處理方法,不受Heisenberg測不準原理制約,可以在時間和頻率上同時達到很高的精度,非常適用于分析突變信號。筆者以薄壁鋁板為研究對象,利用雙重時間尺度的方法,即采用二維傅里葉變換法整體傳播時間尺度,HilbertGHuang變換從單一信號時間尺度,將二者相結合對在鋁板中不同位置采集到的Lamb波信號作數據處理與分析,與半解析有限元法得到蘭姆波的頻散曲線相對照,進而識別與分析鋁板中蘭姆波模態,獲得較高的時間分辨率。
薄板中超聲導波分離模態信號分析方法
一、傳播特性的半解析有限元分析
在邊界自由的固體板中,板材厚度與激勵聲波波長數量級相當時,在板中產生的應力波就是Lamb波.根據薄板兩表面質點振動相位關系,Lamb波分為對稱型Lamb波和反對稱型Lamb波,分別用Sn、An 表示,n 為模態的階次(n=0,1,2,3)。對稱模態和反對稱模態示意如圖1所示,對稱模態中沿著板厚方向中心點對稱的各節點在厚度方向的位移方向相反;而反對稱模態中,沿著板厚方向中心點對稱的各節點在厚度方向的位移方向相同。
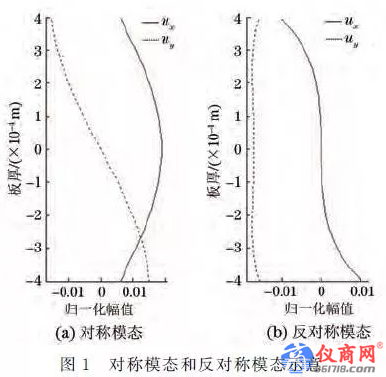
以鋁板中Lamb波的傳播為例,其頻散曲線可采用半解析有限元法求得,只需要在波導介質的截面上作有限元離散,而沿波導介質傳播方向的位移則以簡諧波的振動方式表示,在對介質截面進行有限元離散后,根據哈密頓原理可以推導出導波在介質中的波動方程,求解特征值可以得到波數和頻率的關系,進而繪制出頻散曲線。
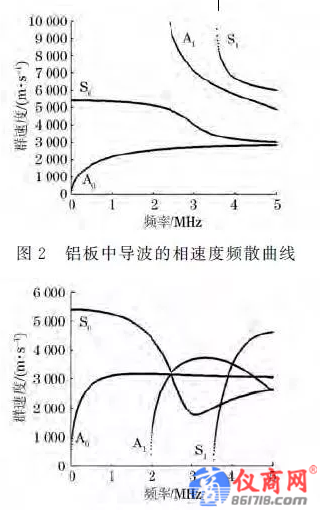
通過半解析有限元法,以鋁板厚度d=0.8mm繪制鋁板中導波的相速度和群速度頻散曲線,得到的模態分布分別如圖2,3所示。
二、二維傅里葉變換
Lamb波在時間和空間上都可以通過二維傅里葉變換轉換為二維各個離散頻率點的頻率G波數能量譜,從而分解出單個Lamb波,并可對其幅值進行測量。單個波動組分在時間上的頻度稱為頻率,而在空間(距離)上的頻度稱為波數.由頻率波數譜中某個波動組分的頻率和波數,可以確定周期和波長。通過對接收信號的二維傅里葉變換,與理論計算得到的波數G頻率的頻散曲線進行對比,從而確定檢測信號中包含的Lamb波模態。
三、HilbertGHuang變換
HilbertGHuang變換是由美國宇航局的Huang等于1998年在經典的Hilbert變換的基礎上提出的.HilbertGHuang變換是一種自適應的信號處理方法,適用于分析非線性非平穩信號,其最大的特點是通過信號的EMD(經驗模態分解),使非平穩信號平穩化,從而使瞬時頻率有意義,進而導出有意義的希爾伯特時頻譜.該方法由EMD與Hilbert譜分析兩部分組成.EMD特別適合處理非線性、非平穩信號,可以把復雜的信號分解為一組按頻率高低排列的固有模態函數(Intrinsic ModeFunction,IMF)之和,每一個IMF所包含的頻率成分不僅與采樣頻率有關,還隨信號變化而變化,因而EMD是一種自適應的信號處理方法。
1、EMD分解
EMD方法是通過特征時間尺度獲得本征模函數,然后用有限個固有振動模態來分解時間序列數據.在EMD分解過程中,信號中最高頻的成分先提取出來,所以第1個IMF分量是從檢測信號中分離出的最高頻成分,依次下去各階IMF的頻率逐漸降低,最后的余項代表了整個時間信號的趨勢.因此原始信號可以表示為所有固有模態分量疊加之和加上余項,即:
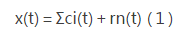
2、HHT譜分析
對式(1)分離的IMF進行希爾伯特變換,可把時間、頻率、幅值畫在三維圖上,簡稱為HHT 譜,記為:
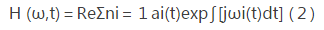
匯總所有IMF分量的HHT譜就得到了原始非平穩信號的Hilbert譜.按照這種方法得到Hilbert譜在聯合的時間G頻域中描述非平穩信號,具有非常高的時頻分辨率。
基于EMD方法分解得到的各個IMF 分量具備實際的物理意義,可以表示信號內部從高頻至低頻的不同部分.同時,根據Hilbert譜中的時間幅值分布,可以轉化為對能量進行有效表征的功率譜或能量譜。
試驗方法
試驗所用鋁板密度為2700kg/m3,厚度d=0.8mm,平鋪在絕緣工作臺上.鋁板中縱波速度為6370m/s,橫波速度為3160m/s。鋁板下方減震處理,超聲探頭位于其上方同側.采用JSR公司DPR300超聲波脈沖發射/接收器提供高壓激勵信號,脈沖振幅313V、能量3.91×10-5J、阻抗333Ω.接入中心頻率f=1.0 MHz的高壓激勵直探頭,直徑1mm的水聽器探頭作為接收端.激發信號接入數字存儲示波器(RIGOLDS1074B)觸發通道,同步信號經過輸出端接入示波器通道1,從而實現波形數字化,試驗裝置如圖4所示。
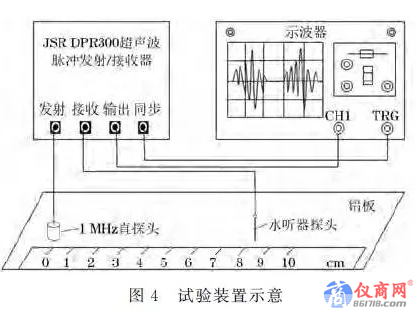
采用少量水作為耦合劑,DPR300 超聲波發射/接收器發出的脈沖激勵發射探頭向鋁板中發射縱波超聲波,并同步觸發數字示波器,水聽器探頭接收的是經傳播后產生的超聲Lamb波信號.在數字示波器上對顯示的信號進行觀察,通過旋轉微調發射探頭,可以獲得顯示幅值最高的信號,示波器對信號進行16次采樣再取平均以提高信噪比.為了減小隨機噪聲對試驗結果的影響,探頭以1mm 的步長變化進行多次采樣,以便根據筆者所用方法進行后續分析和處理。
試驗結果及分析
1、二維傅里葉變換模態分析
將接收傳感器先放在距離發射探頭140 mm處,再使接收傳感器以1mm 步長靠近發射探頭,總采樣組數為140組,得到包含時間和空間信息的蘭姆波信號.鋁板中Lamb波信號的時域圖如圖5所示,數字示波器的采樣頻率為10MHz,采樣點數為600。

從圖5中可以看到,在鋁板中隨著時間傳播的蘭姆波的整體狀態.對所得信號做二維傅里葉變換,得到波數G頻率關系,如圖6(a)所示。
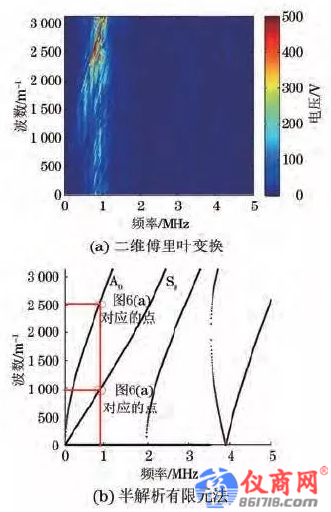
從圖6(a)可以看出,鋁板中傳播模態的頻率為0.98MHz,對應的波數為2500m-1及990m-1,因此在半解析有限元法繪制的波數G頻率關系中可以找到與該頻率、波數值對應的點位于A0 模態和S0模態上,并從圖6(a)中可以看到A0 模態占據了主要能量.因此,通過這種方法在Lamb波整體的傳播時間尺度上可以確定分離的模態及其能量大小.圖7 蘭姆波原始信號時域波形。
2、HilbertGHuang變換模態分析
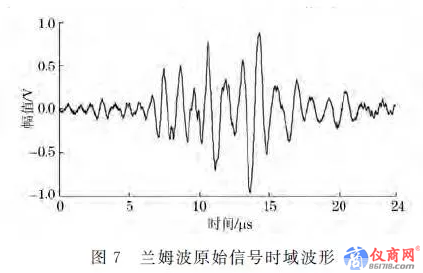
選用1MHz直探頭發射Lamb波,距離換能器中心L=55mm 處以水聽器探頭作為接收端,示波器信號采樣時間24μs,采集到的0.8mm 厚鋁板內Lamb波時域波形如圖7所示,橫軸為時間,縱軸為幅值,以電壓表示,根據圖5中采樣信息可知,在這一位置始波信號并未發生明顯的能量衰減.然而時間軸上的信息則非常復雜,一方面Lamb波主要模態波的波包混疊在一起,體現了其固有的頻散性和多模態特性;另一方面原始信號雖然經過示波器的16次采樣取平均,但是噪聲的頻帶比較寬且存在于整個時間段.因此原始時域波形上各模態峰值并不明顯,難以準確提取獲得有效的分析數據.對原始信號做EMD分解,前4階IMF分量如圖8所示.對照頻譜圖可以看出:
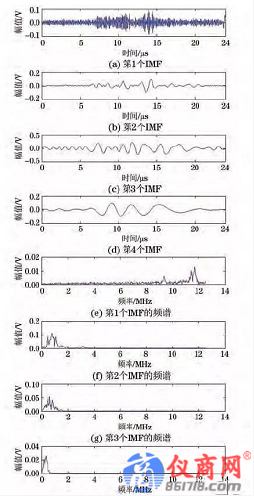
(1)低階的IMF 包含了主要信息,從第4階IMF開始能量非常微弱,與探頭的中心頻率也相差很遠,為低頻干擾信號,可以濾除而不會造成主要信息丟失。
(2)1階IMF為信號中的高頻成分,這其中除了信號本身混疊的高頻分量外,主要為前文所述的環境噪聲。
(3)2階IMF和3階IMF含有絕大部分能量,與原始信號的相關性也最好。
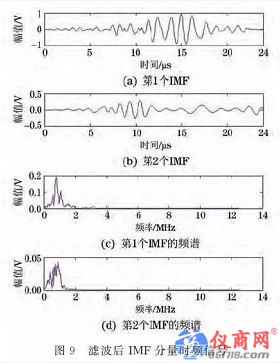
對不同模擬信號以及試驗中采集的其他數據進行研究,可以獲得各階IMF信號變化規律.當原始信號為較清晰的低噪聲信號時,EMD分解后的低階IMF為主要信息成分,高階為其他噪聲;當原始信號有較多的環境噪聲時,低階IMF往往先是高頻噪聲,再高階為其他噪聲,濾波后IMF時頻信號如圖9所示.直接對多模態的Lamb波進行HHT變換易受高頻噪聲影響,分析的結果雜亂[9].因此,對于(2)中所述情況,為了不丟失信息,經過各種去噪方法,采用帶通濾波技術對原信號進行處理之后再進行EMD分解即可濾除高頻環境噪聲。
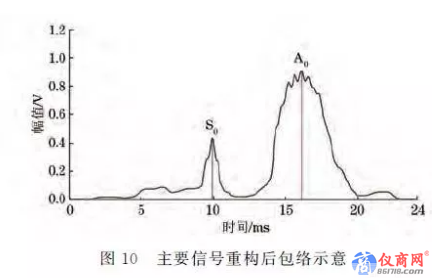
重新分解經過處理后的信號,1階、2階IMF分量即為信號的主要成分,如圖9所示,在中心頻率1MHz附近有兩個波包,需要利用重構算法獲得具有較高信噪比的原始信號[10].因此,對其進行重構,經過希爾伯特變換后,根據幅值(能量)可以做出能量包絡[11],如圖10所示.以包絡的峰值時刻作為信號到達的時間點,從圖中可以更直接地讀出S0 模態和A0 模態的波到達時刻.根據圖2中厚度為0.8mm 鋁板,1MHz中心頻率所對應的A0 模態群速度為vA0 =3244m/s,S0 模態群速度為vS0=5297m/s,由L=55mm 可以計算得出A0 模態到達的理論時刻為16.5μs,S0 模態到達的理論時刻為10.1μs,兩個模態的波形到達的時間差Δt=6.4μs.實際測量A0 模態到達的時刻為16.1μs,S0 模態到達的時刻為9.9μs,時間差Δt=6.2μs.理論數據和實際測量結果基本吻合,說明通過這種方法可以從單一信號時間尺度內準確區分各模態波的到達時間。
超聲波在板狀介質中傳播存在多種模態,為了提高檢測的速度與精度,在圖像處理中對獲取的檢測信號進行模態分析是非常必要的.二維傅里葉變換可以從Lamb波整體的傳播時間尺度上,根據一系列試驗數據定性判定模態及其能量分布;HilbertGHuang變換則可以判定單一時間尺度信號內部不同頻率特征的部分,經過合理的分解濾波重構,對有用IMF進行譜分析的方法可以將信號內不同模態進行定量區分.將這兩種不同時間尺度分析方法結合半解析有限元法的理論數據進行驗證,為超聲導波用于薄板或復雜截面結構的無損檢測提供一種可行的信號分析方法。




















